Prize Bonds are looking attractive alternatives to deposits
- Thread starter Raging Bull
- Start date
Tertonmike
Registered User
- Messages
- 2
Have read right through this thread with great interest. A great effort by dub_nerd and others to impose some sort of mathematical order on the prize bonds proposition, for which much thanks!
I have just run a couple of exercises based on dub_nerd's table on p.13 to assess the chances of achieving or bettering the suggested target return of 1.18% and a slightly higher 1.25% as a control/reference. Please correct me if I am wrong but it seems to me that, as well as allowing for the "lumpiness" of the particular distribution for any given level of investment, the lumpiness of the actual return in prize money has to be taken into account. This is because the actual returns based on €50 prize intervals that meet or better the target varies for each level of investment (actually from 1.19% to 1.5% for a target of 1.18%), consequently the probability of achieving or bettering a fixed target does NOT increase smoothly as the amount invested rises.
My results suggest that the best chances of making 1.18% or better (using €10,000 intervals up to €100,000 as per the chart on p. 13 of the thread) are in fact given by investments of:
1. €80,000 (51.37%)
2. €50,000 (51.08%)
3. €20,000 (50.61%)
In comparison the probability of making 1.18% or better on an investment of €100,000 appears to be only 48.79%.
Using a slightly higher target rate of return of 1.25%, "prize lumpiness" means that the best investment amounts change to:
1. €20,000 (still at 50.61%)
2. €40,000 (46.62%)
3. €60,000 (43.15%)
cf. only 40.71% for €100,000.
Of course this effect may be partly or wholly offset by:
A. The fact that the actual return on investment amounts with a lower probability of hitting/exceeding target may be higher IF the target is met; and/or
B. The point made in previous posts, that with higher investment amounts, the smoothing of the return curve yields a greater chance of just exceeding or just falling short of target.
BUT it seems to be that a decision on the optimum amount to invest in Prize Bonds should not rest on a simple assumption that the probability of making any given target return inevitably and smoothly rises as the amount invested increases.
P.S. Any further work done on the effect of 1 weekly draw for 9,000 prizes vs. 9,000 individual draws p.w.?
I have just run a couple of exercises based on dub_nerd's table on p.13 to assess the chances of achieving or bettering the suggested target return of 1.18% and a slightly higher 1.25% as a control/reference. Please correct me if I am wrong but it seems to me that, as well as allowing for the "lumpiness" of the particular distribution for any given level of investment, the lumpiness of the actual return in prize money has to be taken into account. This is because the actual returns based on €50 prize intervals that meet or better the target varies for each level of investment (actually from 1.19% to 1.5% for a target of 1.18%), consequently the probability of achieving or bettering a fixed target does NOT increase smoothly as the amount invested rises.
My results suggest that the best chances of making 1.18% or better (using €10,000 intervals up to €100,000 as per the chart on p. 13 of the thread) are in fact given by investments of:
1. €80,000 (51.37%)
2. €50,000 (51.08%)
3. €20,000 (50.61%)
In comparison the probability of making 1.18% or better on an investment of €100,000 appears to be only 48.79%.
Using a slightly higher target rate of return of 1.25%, "prize lumpiness" means that the best investment amounts change to:
1. €20,000 (still at 50.61%)
2. €40,000 (46.62%)
3. €60,000 (43.15%)
cf. only 40.71% for €100,000.
Of course this effect may be partly or wholly offset by:
A. The fact that the actual return on investment amounts with a lower probability of hitting/exceeding target may be higher IF the target is met; and/or
B. The point made in previous posts, that with higher investment amounts, the smoothing of the return curve yields a greater chance of just exceeding or just falling short of target.
BUT it seems to be that a decision on the optimum amount to invest in Prize Bonds should not rest on a simple assumption that the probability of making any given target return inevitably and smoothly rises as the amount invested increases.
P.S. Any further work done on the effect of 1 weekly draw for 9,000 prizes vs. 9,000 individual draws p.w.?
Hi TertonMike, glad you're finding it interesting. I've a big project deadline next week so don't have too much time to spend. I'm not totally sure you're interpreting the figures right.
The odds of getting an "average" return or better in a year are always going to sum to about 50% for any investment (except where the investment is so low that the average return is less than a single prize, i.e. below the 5k mark). However, this is not the full story. In fact it's tautological -- the average return is the average because you're equally likely to get more or less than it, and the distribution is symmetrical. (The reason you're probably seeing 48% for 100k is because the table only gives two decimal places so there are rounding errors ... in my spreadsheet version it is more exact.
What you really need to look at is the likelihood of getting, say, only half the average return, or any amount that is not the average. This is what gets less and less likely with a large investment. Big investments generate "smoother" returns. Of course, with smaller investments you're about as likely to get 50% more than the average as you are to get 50% less. The point is, though, you are taking a gamble either way. The idea of the large purchase is to turn it from a gamble into an investment.
Re: the single weekly draw vs. 9,000 I haven't managed to fully analyse it but I have a convincing argument that the odds are extremely little changed from the method I'm already using. Will write a note on it sometime.
Cheers.
The odds of getting an "average" return or better in a year are always going to sum to about 50% for any investment (except where the investment is so low that the average return is less than a single prize, i.e. below the 5k mark). However, this is not the full story. In fact it's tautological -- the average return is the average because you're equally likely to get more or less than it, and the distribution is symmetrical. (The reason you're probably seeing 48% for 100k is because the table only gives two decimal places so there are rounding errors ... in my spreadsheet version it is more exact.
What you really need to look at is the likelihood of getting, say, only half the average return, or any amount that is not the average. This is what gets less and less likely with a large investment. Big investments generate "smoother" returns. Of course, with smaller investments you're about as likely to get 50% more than the average as you are to get 50% less. The point is, though, you are taking a gamble either way. The idea of the large purchase is to turn it from a gamble into an investment.
Re: the single weekly draw vs. 9,000 I haven't managed to fully analyse it but I have a convincing argument that the odds are extremely little changed from the method I'm already using. Will write a note on it sometime.
Cheers.
I finally gave in and purchased €800 (not much I know) in prize bonds today. It was beginning to annoy me and I said sure I 'll give it a try. I might build up to €10,000 but probably wouldn't go any higher.
Don't worry I wont be posting every week, I'll leave that to The Ghoul.
Don't worry I wont be posting every week, I'll leave that to The Ghoul.
Unfortunately the reason you probably wont be posting is due to not winning anything! As explained above, the less PB you have, the chanced of winning drop dramatically. You need in excess of 10K really.
As explained here: http://www.askaboutmoney.com/showpost.php?p=1398663&postcount=248
As explained here: http://www.askaboutmoney.com/showpost.php?p=1398663&postcount=248
As u123 says, this is pointless. You will win a €50 prize on average less than once every five years. But there is a significant chance you could go 10 or 20 years without a prize (you could always win in less than five, of course). The question is, do you want a significant chance of getting nothing? A deposit rate of 1% after tax will get you almost €50 in five years. Why would you take a significant risk of getting nothing?
As an investment (as opposed to a gamble) the only way that prize bonds make sense is that the average return is somewhat above typical after-tax deposit rates and, (this is the important bit) for very significant investments -- meaning at least multiple tens of thousands -- you have a good chance of getting close to the average return. Caution is not what you want with prize bonds -- paradoxically it makes good sense to buy €100,000 worth, but none at all to buy €100 worth.
Being a prize bond investor, I follow this thread with great interest!
I first started buying prize bonds (in small amounts, usually around IR£100 or so) from around 1989 onwards. Since then I have built-up a nice 'portfolio' of bonds in varying amounts....the largest being a recent €20k purchase. My question is - Would I be better off cashing-in all my bonds and making one large bond purchase using the full amount of the cashed-in bonds?
It would seem to be a good idea based on the discussions on this thread regarding 'larger amounts = better returns' ?!
I first started buying prize bonds (in small amounts, usually around IR£100 or so) from around 1989 onwards. Since then I have built-up a nice 'portfolio' of bonds in varying amounts....the largest being a recent €20k purchase. My question is - Would I be better off cashing-in all my bonds and making one large bond purchase using the full amount of the cashed-in bonds?
It would seem to be a good idea based on the discussions on this thread regarding 'larger amounts = better returns' ?!
The better returns refer to the expected returns for a person being the sum total of the expected return of each individual prize bond held. If you held all of the prize bonds ever issued then you would win all of the prizes. When the prize bonds were purchased is immaterial, although there is a reference earlier in this thread to newer bonds winning more often. Seems to be a conspiracy theory though
Selling all your bonds and buying them back again wouldn't make them a larger amount.
So, Ghoul, if I'm counting it right, after a year your €50 prizes add up to €1,100 or 1.1%, i.e. within a whisker of the average return. On top of that you have the nice bonus of the 2 x €100, which is three times the 0.65 of them you should win on average (although you won them before Jan 2014, when the number of €100 prizes went down significantly). And the icing on the cake is the wholly fortuitous €1,000 prize which was a one in 80 chance. That brings you to a 2.3% tax free return, which is pretty much double what you might reasonably have expected, and grosses up to the equivalent of a 4.18% return from a taxable deposit. Not bad at all!
I have always assumed that it's one big draw and every bond is entered into that and can only be pulled maximum once every week. Prize bonds have been going for a long time, longer than the widespread availability of computers, haven't they - it might be completely unrealistic but I've always had this image of men in brown suits with the equivalent of a big giant hat, pulling numbers out while someone on the side with a clipboard carefully notes them down.
So, I promised I'd come back to this. Haven't had time to think about how to calculate it more correctly. But I thought I might set out the calculations I was using for odds so far, and see if any maths guru out there can help amend it for the situation Janet is talking about, where each bond can only win once per week.
The question I originally wanted to answer was "what are the odds of winning a particular number of times in a year, with a particular number of prize bonds?". I decided I should start with some simpler examples. What are my chances of winning two out of three coin tosses? The chances of anything happening are: the number of ways the given thing could happen, divided by the total number of things that could happen. For example, the chance of throwing a three on a dice are: one way a three can come up, out of six different numbers that could come up, i.e. 1/6. What about our three coin tosses? I can write down the possible outcomes as a sequence of heads (H) and tails (T):
1: H H H
2: H H T
3: H T H
4: H T T
5: T H H
6: T H T
7: T T H
8: T T T
Now I just count the number of outcomes for which there are two heads -- outcomes 2,3 and 5, so the odds are 3/8. Note, this is the odds of getting exactly two heads. For the odds of getting at least two heads, we have to add in outcome number one where we get three heads, for odds of 4/8 or 1/2.
Ok, now let's generalise this problem. What are the chances of getting exactly k heads out of n coin tosses. For the three-toss two-head problem above I just had to count all the ways I could choose two slots to be heads out of three different positions. Now I want to choose k slots out of n different positions. This is sometimes expressed as "n Choose k" and there is a well known formula for it in combinatorics:
The exclamation mark notation means "factorial" which in turn means "multiply all the numbers from n down to 1", so for example 5! = 5 x 4 x 3 x 2 x 1. Let's see how it works out for our previous example of two heads out of three tosses, i.e. "3 choose 2":
That matches what we found -- there are three ways to choose two slots to be heads out of three coin tosses. But we're looking for odds, so what's the total number of ways that n coin tosses can turn out? That's easy -- there are two possible outcomes each time (H or T) so for n tosses it's:
So finally, the odds of k heads out of n coin tosses are:
Now let's generalise some more. When we wrote down all the possible heads (H) and tails (T) outcomes, we could have chosen any symbol for heads and tails. Let's do it again and choose 0 and 1:
1: 0 0 0
2: 0 0 1
3: 0 1 0
4: 0 1 1
5: 1 0 0
6: 1 0 1
7: 1 1 0
8: 1 1 1
If you know what binary numbers are, i.e. numbers in base 2, you can see that our coin toss problem is exactly the same as saying: "how many 3-digit base-2 numbers are there with exactly 2 zeros?", or more generally: "how many n-digit base-2 numbers are there with exactly k zeros?". We could generalise even more by working in any base, b. How many n-digit base-b numbers are there with exactly k zeros?
It's quite easy to generalise our existing formula for this. First we have to realise that the total number of possible outcomes is now
So finally, the number of n-digit base-b numbers with exactly k zeros is:
At this stage you may be wondering what all this has to do with Prize Bonds. Well, we've now got everything we need to answer our original question. We look at the number of prizes every year and notice that the number of €50 prizes so vastly outnumbers all the others, that as a first approximation we can ignore every other type of prize. The prize bond website tells you how to work out the number of €50 prizes ... it's about 470,000 in a year. Now, using my flawed logic, there are 470,000 draws each year. (In reality there are 52 draws with about 9,000 prizes in each draw but bear with me). Let's say you are entered in each of 470,000 draws. What are your chances of winning each draw? It is your amount invested divided by the total prize bond fund ... that's the fraction of the total prize bonds you hold. For example, you have €100k invested, the total fund is €2 bn, so you have a 1/20,000 chance in each draw. That means there's one chance you'll win it, and 19,999 chances someone else will win it.
Ok, so let's pretend each draw is one digit in a vast 470,000 digit number. There are 20,000 different way each draw could come out -- one of which represents a win for you, so let's say a win for you is the zero digit in a base 20,000 number. What are the odds of you winning, say, 23 times? This is a problem we know how to solve! It's the number of 470,000 digit numbers in base 20,000 with exactly 23 zeros! And that's what our formula gives us:
There's some crazy big numbers to deal with there -- bigger than a spreadsheet like Excel can work with directly -- but it is possible to get an answer, and in this case it works out to a little worse than 1/12 or 8.08%. That's the odds of winning exactly 23 x €50 prizes with €100k invested. You can work out the odds for any other number of wins and investment amounts using the same formula, which is what I've done throughout this thread.
Now, the way we've modelled this approach, there is some tiny but non-zero chance that your bonds could win all 470,000 x €50 prizes. But we suspect that actually, each bond can only win once per week so we have to model it differently. I'm not sure exactly how, but I have a germ of an idea. But maybe someone out there knows an easy way? How's that for a challenge.
Correct (and I wouldn't be re-purchasing the exact same bonds
)What I obviously meant was purchasing a large 'block' of bonds.....as opposed to my current 'spread' of bonds.
Correct (and I wouldn't be re-purchasing the exact same bonds
What I obviously meant was purchasing a large 'block' of bonds.....as opposed to my current 'spread' of bonds.
You obviously didn't believe me when I responded to the same question by PM.
You're suggesting that if you held tickets 84 and 86 in a raffle you could improve your odds by swapping them for tickets 87 and 88 because the latter is a 'block'. Ok, suppose the competition organisers agree that you can write any number you want on the back of your tickets as long as they're not taken already, and they'll do the same with the duplicate tickets in the drum that they will do the draw from. You write 87 and 88 on the back of your tickets and they do likewise with tickets 84 and 86 in the drum. You have the same physical tickets as before. Have your chances improved?
Or if you choose 1 and 2 on a dice, you're saying your numbers will come up more often on repeated rolls than the guy who chooses 3 and 5. What if I then took your dice and repainted the faces on it, so that what used to be 1 and 2 are now 3 and 5, and vice versa. Are you saying I have now changed the odds on different physical faces coming up, just by labelling them something different?
Or again, if an asteroid is about to crash into a town in Ireland and kill one of the inhabitants, it's more likely to happen in a town where everyone's social security numbers were issued from the same block?
Why does that last example seem even sillier than the others? -- because the selection criteria (being essentially random) have nothing to do with the identities of the population being selected from. But actually, it's the same in all the examples. In all cases -- Prize Bonds included -- you should just think of the number designations as labels on the physical objects. Changing the labels can't change the odds.
(If we were to get technical, we would say the countable additivity property from Kolmogorov's third probability axiom guarantees that any same-sized subsets of events with equal probabilities sum to the same probability... but that's just a fancy way of saying any n Prize Bonds has the same likelihood of coming up as any other n Prize Bonds).
I said I had a germ of an idea. As a first step in looking at the difference between your chances if your Prize Bonds are entered in a separate draw for every prize, vs. a single draw for n prizes per month, I looked at the chances of winning at least once in a month.
If each draw was independent, i.e. bonds are "replaced in the giant drum" after each draw, then the chance of not winning each draw is the fraction of bonds not held by you, and the chance of not winning any draw is simply that number raised to the power of the number of draws. To put some numbers on it, if you hold 1/20000 of all Prize Bonds (equivalent to €100k investment) and there are 9,000 x €50 prizes each month, then your chances of not winning in a month are:
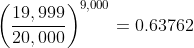
Now let's look at the chances if winning bonds are not replaced. Here we have to look at the number of different ways in which we could draw a bond that isn't yours. Your €100k investment represents 16,000 bonds out of a total of 320,000,000 issued. So the number of ways of choosing 9,000 winning bonds, none of which are yours, is:
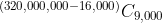
And to get the chances of that happening, we divide by the total number of ways that 9,000 bonds could be drawn:
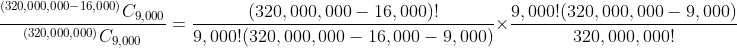
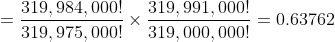
Hey presto! The odds work out the same to five decimal places under both scenarios (and I don't know how much of the differences beyond that are rounding errors in the calculations). These are the odds of you not winning in a month, so your odds of winning at least once, are: (1 - 0.63762) = 0.36238. That is, you have a 36.238% chance of winning at least once in a given month.
Intuitively, the fact that the numbers are so close by either method of calculation (for one draw per month vs. 9,000 draws per month) is not very surprising for such huge numbers and such a relatively small fraction of total bonds held. It convinces me that my other calculations throughout this thread would be very little affected either. Unfortunately, I don't (yet) have the mathematical acumen to come up with an exact calculation to replace them. (The difficulty is combining the odds per month to come up with the odds of winning a given number of times per year). But I believe the bottom line is that all the odds stated so far are correct to a high degree of accuracy regardless of the method of conducting the draw.
If each draw was independent, i.e. bonds are "replaced in the giant drum" after each draw, then the chance of not winning each draw is the fraction of bonds not held by you, and the chance of not winning any draw is simply that number raised to the power of the number of draws. To put some numbers on it, if you hold 1/20000 of all Prize Bonds (equivalent to €100k investment) and there are 9,000 x €50 prizes each month, then your chances of not winning in a month are:
Now let's look at the chances if winning bonds are not replaced. Here we have to look at the number of different ways in which we could draw a bond that isn't yours. Your €100k investment represents 16,000 bonds out of a total of 320,000,000 issued. So the number of ways of choosing 9,000 winning bonds, none of which are yours, is:
And to get the chances of that happening, we divide by the total number of ways that 9,000 bonds could be drawn:
Hey presto! The odds work out the same to five decimal places under both scenarios (and I don't know how much of the differences beyond that are rounding errors in the calculations). These are the odds of you not winning in a month, so your odds of winning at least once, are: (1 - 0.63762) = 0.36238. That is, you have a 36.238% chance of winning at least once in a given month.
Intuitively, the fact that the numbers are so close by either method of calculation (for one draw per month vs. 9,000 draws per month) is not very surprising for such huge numbers and such a relatively small fraction of total bonds held. It convinces me that my other calculations throughout this thread would be very little affected either. Unfortunately, I don't (yet) have the mathematical acumen to come up with an exact calculation to replace them. (The difficulty is combining the odds per month to come up with the odds of winning a given number of times per year). But I believe the bottom line is that all the odds stated so far are correct to a high degree of accuracy regardless of the method of conducting the draw.
No offence regarding your advice to me via PM....it was/is most appreciated
The reason I posed the question is due to the many comments here regarding larger investments giving 'better' returns ....e.g. your post above.
No offence taken. But my first answer is the simplest and most correct -- changing your numbers isn't a larger investment. Somewhere along the way you conflated larger 'block' with larger investment. Sorry if I misled by saying it makes sense to buy €100k but not €100. The €100k could be made of a thousand separately purchased hundreds ... it's the total that counts. Intuitively -- and also as a matter of fact, according to Kolmogorov's third axiom -- each little piece of your purchase contributes additively to your overall chance of winning.
Thanks for all the informative and interesting posts on Prize Bonds!
When cashing in PBs is it better to send by registered post or to simply use the freepost option for value > €40K? (photocopies of all Prize Bonds will be kept).
According to An Post website "Additional insurance is available for items posted within the Republic of Ireland. A charge of €4 is applicable for cover up to €1,500 and a charge of €5 for cover up to €2,000." - doesn't seem worthwhile...
When cashing in PBs is it better to send by registered post or to simply use the freepost option for value > €40K? (photocopies of all Prize Bonds will be kept).
According to An Post website "Additional insurance is available for items posted within the Republic of Ireland. A charge of €4 is applicable for cover up to €1,500 and a charge of €5 for cover up to €2,000." - doesn't seem worthwhile...